Temperatura: 32 grados Celsius, estas dando vueltas buscando parqueos libres en tu carro cuyo aire acondicionado ya tuvo sus mejores años. Preocupado, revisas tu celular y notas los mensajes de tu jefe preguntando si ya estás en camino, continúas dando vueltas al sector buscando un parqueo que por lo menos esté un poco más cercano al lugar de la reunión para así no tardar más tiempo caminando, pero en qué momento paras de buscar y ya te parqueas en el siguiente lugar disponible?

Esta situación en algún momento nos ha pasado a todos, y en el mundo de las matemáticas es uno de los problemas más conocidos y estudiados. Este curioso acertijo matemático es conocido como un problema de detención óptima y tuvo su primera publicación impresa en una edición del Scientific American en 1960. Sin embargo, la estructura original del problema no tenía nada que ver con parqueos, sino en la elección de una secretaria/io para un nuevo puesto.
Imagina que estás entrevistando a un grupo de candidatos para un puesto de secretaria/io y que tu objetivo es maximizar las posibilidades de contratar al mejor candidato del grupo. Aunque no tienes ni idea de cómo asignar puntuaciones a cada uno de los candidatos, denominado un problema con información limitada, puedes juzgar fácilmente a cuál prefieres.
El primer paso es entrevistar a los candidatos en orden aleatorio, de uno en uno, puedes decidir ofrecer el trabajo a un candidato en cualquier momento y se garantiza que acepte, dando por terminada la búsqueda. Sin embargo, si decides no contratar a un candidato, éste desaparece para siempre. Cómo te aseguras de que la decisión que tomas es la más acertada para obtener al mejor candidato?

Este problema, aunque parezca tan simple, tiene un sin número de aplicaciones en el mundo de hoy desde como encontrar un parqueo, o vender tu casa por un precio óptimo, también para arrendar un apartamento, hasta como encontrar a tu media naranja, entre otros. Tiene un rango impresionante de aplicaciones y también complicaciones si agregamos diferentes tipos de nuevas variables; ahora si de vuelta al problema.
Si elegimos a la primera candidata que entrevistamos, no existiría el dilema, ya que por definición no tendríamos contra quien compararla y por ende sería la mejor calificada. Si decidimos continuar en nuestra búsqueda y vamos a la siguiente candidata, perdiendo la opción de volver a la primera entrevistada, tendríamos probabilidades 50/50 de que la segunda candidata sea mejor que la primera (simplemente lo es o no lo es). Y qué pasa si no estamos convencidos y decidimos continuar con la búsqueda? Es decir, dejamos pasar la oportunidad de contratar a la segunda para entrevistar a una tercera. Y qué pasa si decidimos continuar con una cuarta? Y luego una quinta?
Rápidamente nos damos cuenta de que a medida que continuemos entrevistando a más candidatos nuestras probabilidades de encontrar al candidato perfecto empiezan a disminuir. Si para el segundo candidato las probabilidades eran de 50/50, para el quinto las probabilidades bajan a 1/5. Así que cual es el punto óptimo que balancea nuestro interés de seguir buscando el mejor candidato posible o el temor a que nunca lo encontremos y ya lo hayamos pasado?
Al parecer, existe una respuesta a este enigma y se resume en un número: 37%. A medida que incrementa la muestra, resulta que el momento óptimo para dejar de seguir buscando opciones y tomar una decisión es cuando hayas evaluado al 37% de la población. Con esto nace la ahora conocida como Regla del 37%: entrevista al 37% de los posibles candidatos, no elijas a ninguno, y elige al siguiente.

Esto significa que incluso al detenernos en nuestra búsqueda de la manera más optima posible, aun así no elegiríamos al mejor candidato el 63% de veces. Terribles probabilidades no? Pero, si no nos detenemos de la manera más optima, es decir si elegimos a alguien de forma aleatoria, en una población de 100 candidatos nuestro chance de elegir al mejor fuera del 1%, si la población es un millón de candidatos nuestro chance seria de 0.0001%; ahora sí el 37% se ve mucho más interesante.
Incluso esta simple regla la podemos aplicar al momento de buscar nuestra pareja, tanto para la cantidad de posibles parejas a analizar o el tiempo que pensamos que vamos a estar buscando una pareja.
Esto lo aplicó el profesor de Investigación de Operaciones de Carnegie Mellon, Michael Trick. Puso como meta buscar a su pareja desde los 18 años de edad hasta los 40 años, y luego de aplicar la regla del 37%, que indicaba el momento óptimo para ya parar de buscar y decidirse con quien casarse sería a los 26 años, decidió tomar el gran salto. Al parecer una persona que hace lo que predica.

Regresando a nuestro dilema inicial de si parqueamos en el siguiente espacio vacío que veamos o no, podemos ver que este dilema es también un problema de detención óptima y se deriva del original revisado anteriormente, pero utilizando como variable principal el nivel de utilización del parqueo.
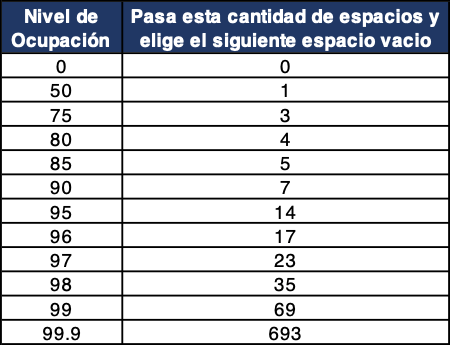
El profesor de UCLA de Planificación Urbana, David Shoup, argumenta que idealmente las ciudades deberían construir sus parqueos modelándolos como un problema de detención óptima.
Las ciudades deberían darse cuenta que es normal y deseable que ciertos sectores, aunque sean muy concurridos, y por ende traigan buenos ingresos a los Municipios por el uso de los parquímetros, tengan sus parqueaderos ocupados hasta un 85% de nivel de ocupación y nunca en un 100%. Ya que más allá de eso significa que los conductores deben pasar más tiempo dando vueltas buscando parqueo. Lo que se traduce en pérdida de tiempo, de atención, gasto de combustible, y genera congestión en las ciudades y contaminación.
Así que la próxima vez que estes dando vueltas buscando parqueo, fíjate más o menos en que tan lleno está y acuérdate de detenerte óptimamente.
References
Algorithms to Live By: The Computer Science of Human Decisions by Brian Christian and Tom Griffiths
